As an example, lets look at the A major scale. As the name suggests, the scale starts on the note ‘A’, and contains the following 7 notes:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| A | B | C# | D | E | F# | G# | A |
| (root) | (octave) |
‘A’ is referred to as the root note, and we arrive back at A (the octave) after the 7th note (G#), an octave higher. If we refer to our Chromatic Scale (immediately below), we can see the Step Pattern that this scale uses:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 1 |
| A | A# | B | C | C# | D | D# | E | F | F# | G | G# | A |
| (Bb) | (Db) | (Eb) | (Gb) | (Ab) |
The interval between the 1st and 2nd notes of the A major scale (A and B) is two semitones (A to A# = 1 semitone, A# to B = 1 semitone), or one whole tone. On the guitar this would be an interval of two frets, since one fret = one semitone.
If we write out all the intervals like this for all the notes of the A major scale, we find that:
| 1st (A) | to | 2nd (B) | = 1 tone | (2 frets) |
| 2nd (B) | to | 3rd (C#) | = 1 tone | (2 frets) |
| 3rd (C#) | to | 4th (D) | = 1 semitone | (1 fret) |
| 4th (D) | to | 5th (E) | = 1 tone | (2 frets) |
| 5th (E) | to | 6th (F#) | = 1 tone | (2 frets) |
| 6th (F#) | to | 7th (G#) | = 1 tone | (2 frets) |
| 7th (G#) | to | octave (A) | = 1 semitone | (1 fret) |
So we have found the Step Pattern for a major scale:
| tone | tone | semitone | tone | tone | tone | semitone | |||||||||
| A | ^ | B | ^ | C# | ^ | D | ^ | E | ^ | F# | ^ | G# | ^ | A | |
| Frets: | 2 | 2 | 1 | 2 | 2 | 2 | 1 |
On the guitar, we could play it on the G string (3rd string) like this:
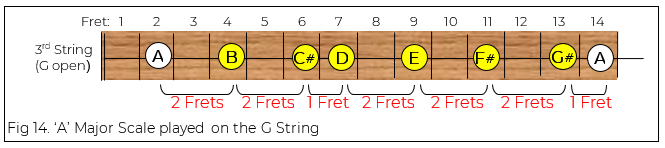
Listen:
This applies to all major scales. So, if we wanted to work out the scale of C major, for example, referring to the chromatic scale presented earlier, we would end up with:
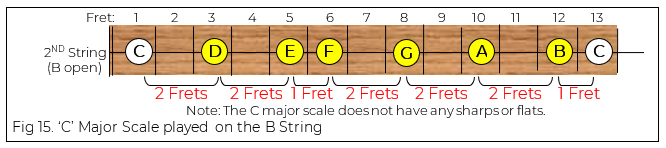
Listen:
Exercise: Try working out the major scales for B, D, E, F, G and C#.