So far, I have only outlined diatonic intervals. These are not the only intervals that exist, there are also intervals between sharp and flat notes to consider. Here is the full list of both simple and compound intervals:
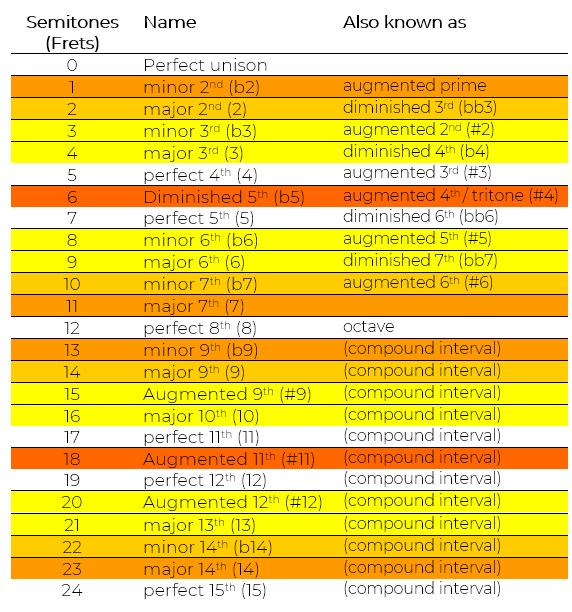

Intervals from 0 up to 12 semitones are simple intervals. Intervals above 13 semiitones are compound intervals.
After 12 semitones (the perfect 8th, or octave) we continue naming the intervals in numerical order ie. 9th‘s up to 15th‘s.
So to play a major 9th interval, we would play the root note and the major 2nd note an octave higher.
Here are some rules regarding intervals:
- A major interval reduced by one semitone becomes a minor interval.
- A major interval increased by one semitone becomes an augmented interval.
- A minor interval reduced by one semitone becomes a diminished interval.
- A minor interval increased by one semitone becomes a major interval.
- A perfect interval reduced by one semitone becomes a diminished interval.
- A perfect interval increased by one semitone becomes an augmented interval.
INVERTING INTERVALS
Intervals can be inverted, so that the higher note becomes the lower note, and vice versa. When we invert an interval, we come up with a new interval, based on the following rules:
To name the inverted interval, subtract the degree of the original interval from 9 (e.g. a 7th becomes a 2nd, a 6th becomes a 3rd, a 4th becomes a 5th, and so on).
A perfect interval, when inverted, is still perfect.
A major interval, when inverted, becomes minor, and a minor interval becomes major.
An augmented interval, when inverted, becomes diminished, and a diminished interval becomes augmented.